Pascal's Triangle, Factoring, and Modular Arithmetic

Greetings,

I haven't updated in a while, in part because we've mostly been doing contests or going over contest problems.

Last week: Pascal's Triangle

Last week, in order to take a break from problems, we played around with Pascal's triangle. I based a lot of the lesson on Math is Fun's Pascal's Triangle page.

I printed some hex paper for us to use, and we built our own triangles.

First, we looked for patterns on the diagonal. We found the first two trivial ones. The third is a pattern we've looked at before: triangle numbers. The fourth we talked about briefly — tetrahedral numbers. It's like a 3-D version of triangle numbers. That's as far as we went with that.

We looked at some Sierpinski Triangle patterns, shading in evens for one iteration, and shading differently based on the remainder mod 3 for another. Here is my remainder mod 3 picture, where white is for 0, green is for 1, and blue is for 2.

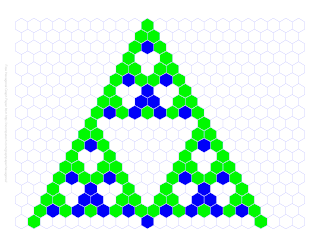
Without using the term modulus, we talked about how for these triangles we don't need to know the value of the numbers in the hex to fill in the remainders, but this foreshadowed modular arithmetic, which I will return to below.

I briefly talked about how the Pascal numbers showed how many ways to flip coins heads or tails. For example, with a single coin flip, there is one way to get one head, and one way to get one tail, which maps to the second line in the triangle. With two flips, There is one way to get two heads, two ways to get one head and one tail, and one way to get two tails, which corresponds to the third line. We talked about how this means that the probability of one head and one tail is more probable than two of one kind, and so even though there are three possible outcomes, they aren't equally likely.

Relatedly, we talked about the number of ways to get to each hex if you start at the top and always go down.

Today: Factoring, and a little Modular Arithmetic

Prime factorisation

We started with finding prime factors in tree fashion:

We did 12, 51, and 156.

Then we worked on the following problems:

1. 12 has 6 factors. Find the smallest natural number with exactly 6 factors.
2. What is the largest odd factor of 90?
3. If N is the product of primes p, q, r, how many factors does it have?
4. How many numbers <= 100 have exactly 3 factors?

Factoring riddles

These do not necessarily have unique solutions. I got them from Bridges in Mathematics.

1. I am a common factor of 27 and 45. I am an odd number. When you multiply me by 3, you get a number greater than 10. What number am I?
2. I am a common factor of 36 and 48. I am also a factor of 30. I am an even number. I am divisible by 3. What number am I?
3. I am a common factor of 60 and 100. I am an even number greater than 4. I am divisible by 4. What number am I?
4. I am an odd number. I am a common factor of 135 and 210. I am greater than 7. What number am I?

Introducing Modular arithmetic

We recalled the work with Sierpinsky triangles and mod 3 arithmetic.

Then we worked on a couple of variations of the following problem:

Suppose we have a circle with 6 points on it labelled 0 through 5. If we start at the point labelled 0, which of the numbers between 1 and 5 can we keep adding and eventually land on all six points?

We also tried it for an 8 point circle, and started to make generalisations.

Next week we'll see what else what can find out about that problem.